Quaternion Slerp

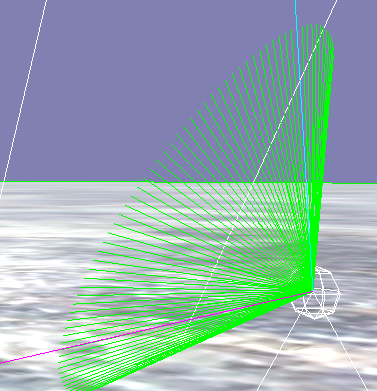
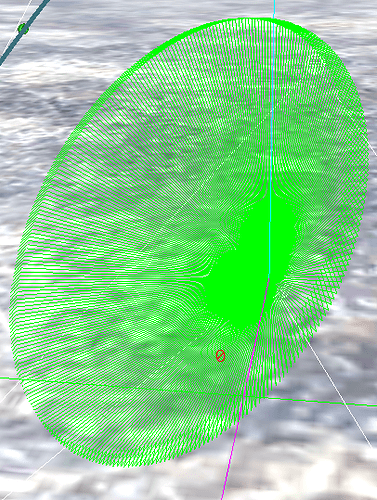
Per Wikipedia, I was under the impression that Quaternion::Slerp was supposed to return points along a great-circle arc between two quaternions. Could someone explain why there seems to be a cone, and not a disk, formed when tracing out the path followed by Slerp? Or point out where I’ve made a mistake?

auto v = Vector3::FORWARD;
auto dr = scene_->GetComponent<DebugRenderer>();
for (int i = 0; i <= 100; ++i)
{
    dr->AddLine({0,0,0.0},Quaternion(v,Vector3::UP).Slerp({v,Vector3::RIGHT},0.03*i) * v,Color::GREEN,false);
//                dr->AddLine({0,0,0.01},Quaternion{90,Vector3::UP}.Slerp({-90,Vector3::RIGHT},0.03*i) * v,Color::RED,false);
}
dr->AddLine({0,0,0.0},Quaternion(v,Vector3::UP).Slerp({v,Vector3::RIGHT},0) * v * 2,Color::CYAN,false);
dr->AddLine({0,0,0.0},Quaternion(v,Vector3::UP).Slerp({v,Vector3::RIGHT},1) * v * 2,Color::MAGENTA,false);

I think I figured it out - I think it has to do with the roll portion of the rotation - you can see how adding rotated vectors that point up behave going around the edge that they are symmetric.

auto v = Vector3::FORWARD;
for (int i = 0; i <= 300; ++i)
{
    dr->AddLine({0,0,0.0},Quaternion(v,Vector3::UP).Slerp({Vector3::RIGHT,Vector3::BACK},0.01*i) * v,Color::GREEN,false);
}
dr->AddLine({0,0,0.0},Quaternion(v,Vector3::UP).Slerp({v,Vector3::RIGHT},0) * v * 2,Color::CYAN,false);
dr->AddLine({0,0,0.0},Quaternion(v,Vector3::UP).Slerp({v,Vector3::RIGHT},1) * v * 2,Color::MAGENTA,false);

auto v2 = Vector3::UP*0.1;
for (int i = 0; i <= 300; ++i)
{
    auto q = Quaternion(v,Vector3::UP).Slerp({Vector3::RIGHT,Vector3::BACK},0.01*i);
    dr->AddLine(q * v,q*(v+v2),Color::GREEN,false);
}
{
    auto q = Quaternion(v,Vector3::UP).Slerp({v,Vector3::RIGHT},0);
    dr->AddLine(q * v * 2, q*(v*2+v2),Color::CYAN,false);
    q = Quaternion(v,Vector3::UP).Slerp({v,Vector3::RIGHT},1);
    dr->AddLine(q * v * 2, q*(v*2+v2),Color::MAGENTA,false);
}

Okay-curving407×539 344 KB